
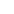

一、分式的乘方和乘方法则
1、分式的乘除
(1)乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为积的分母。
用式子表示为$frac{a}{b}·frac{c}{d}=frac{a·c}{b·d}$。
(2)除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
用式子表示为$frac{a}{b}÷frac{c}{d}=frac{a}{b}·frac{d}{c}=frac{a·d}{b·c}$。
(3)乘方法则:一般地,当$n$是正整数时,
$left(displaystyle{}frac{a}{b}right)^n=$$begin{matrix} underbrace{displaystyle{}frac{a}{b}·frac{a}{b}·cdots·frac{a}{b} }n个 end{matrix}=$$begin{matrix}n个 overbrace{begin{matrix} underbrace{displaystyle{}frac{a·a·cdots·a}{b·b·cdots·b}} n个 end{matrix}} end{matrix}=$$displaystyle{}frac{a^n}{b^n}$,即$left(frac{a}{b}right)^n=frac{a^n}{b^n}$。
即分式乘方要把分子、分母分别乘方。
2、分式的加减
类似分数的加减,分式的加减法则是
(1)同分母分式相加减,分母不变,把分子相加减。
即:$frac{a}{c}±frac{b}{c}=frac{a±b}{c}$。
(2)异分母分式相加减,先通分,变为同分母的分式,再加减。
即:$frac{a}{b}±frac{c}{d}=frac{ad}{bd}±frac{bc}{bd}=frac{ad±bc}{bd}$。
二、分式的乘方的相关例题
$frac{x^2-1}{x+1}·frac{x^2-x}{x^2-2x+1}=$___
A.$x$ B.$2x$ C.$x^2$ D.$2x^2$
答案:A
解析:原式$=frac{(x+1)(x-1)}{x+1}·frac{x(x-1)}{(x-1)^2}=x$。故选A 。

